Who am I, you ask?
I am currently a third-year PhD student in the department of statistics (LPSM) at Sorbonne Université,
under the supervision of Anna Bonnet (LPSM) and Maxime Sangnier (LPSM).
My PhD is part of the doctoral program of the Sorbonne Center for Artificial Intelligence (SCAI).
Research
Preprints
-
"Spectral analysis for noisy Hawkes processes inference", A. Bonnet, F. Cheysson, M. Martinez Herrera, M. Sangnier, Submitted, 2024. Github
Pdf Github
Published papers
-
"Inference of multivariate exponential Hawkes processes with inhibition and application to neuronal activity", A. Bonnet, M. Martinez Herrera, M. Sangnier, Statistics and Computing, 2023. Github
Pdf Github -
"Maximum Likelihood Estimation for Hawkes Processes with self-excitation or inhibition", A. Bonnet, M. Martinez Herrera, M. Sangnier, Statistics and Probability Letters, 2021. Github
Pdf Github
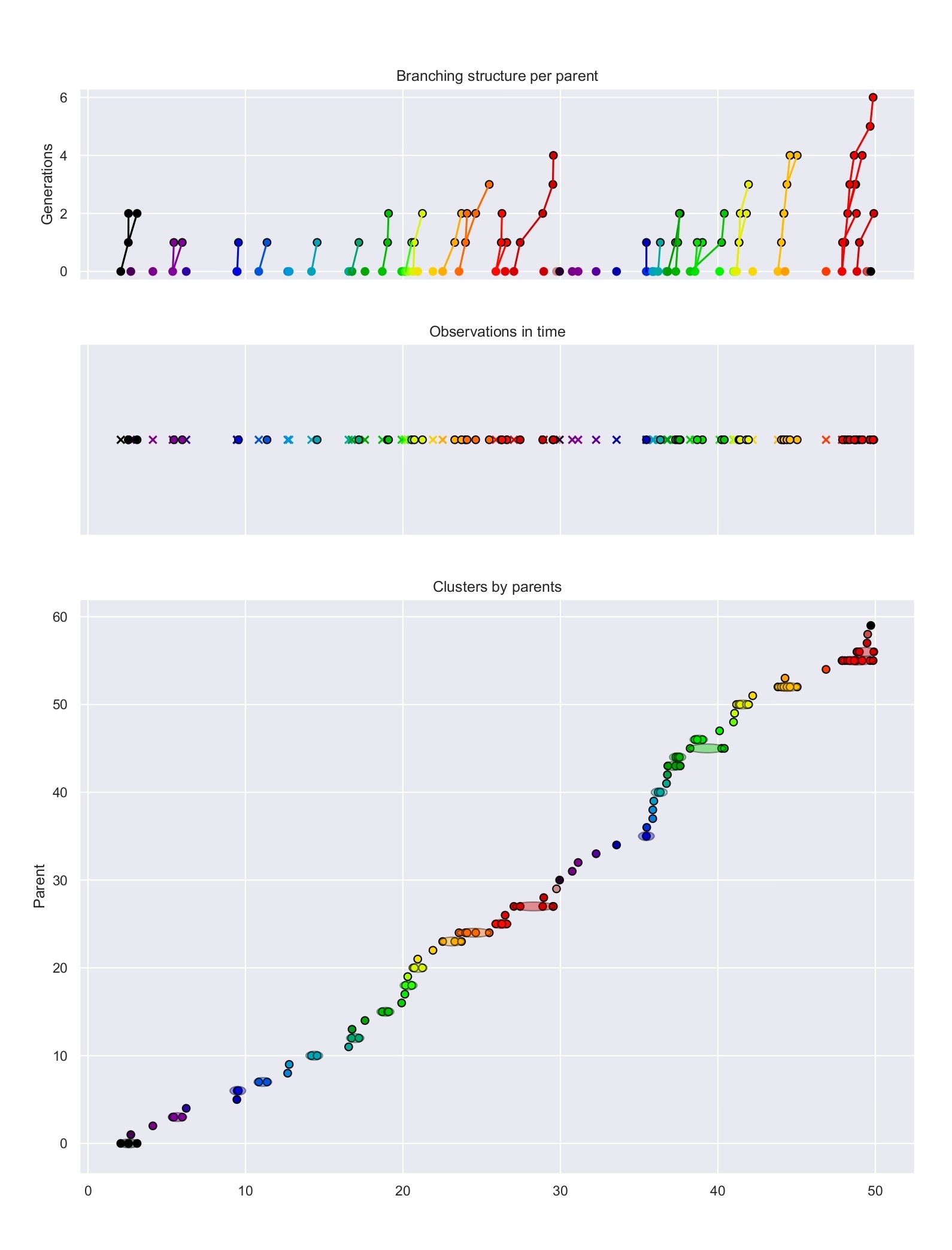
Structures of branching and clustering for Hawkes processes.
Talks
- 55e Journées de Statistique (JdS), Bordeaux, France, Mai 2024.
- 54e Journées de Statistique (JdS), Brussels, Belgium, July 2023.
- PhD students seminar at LPSM, Sorbonne Université, Paris, France, November 2022.
- Lille Days in Point Processes and Stochastic Geometry, Lille, France, Octobre 2022.
- PhD workshop on Artificial Intelligence, Sorbonne Université, Paris, France, Octobre 2022.
- (Invited) SIAM Annual Meeting (AN22), Pittsburgh, Pennsylvania, U.S.A., July 2022.
- Rencontres des Jeunes Statisticien.ne.s (RJS), Porquerolles, France, April 2022.
- SCAI doctoral Workshop, Sorbonne Université, Paris, France, Octobre 2021.
- PhD students seminar at LPSM, Sorbonne Université, Paris, France, Octobre 2021.
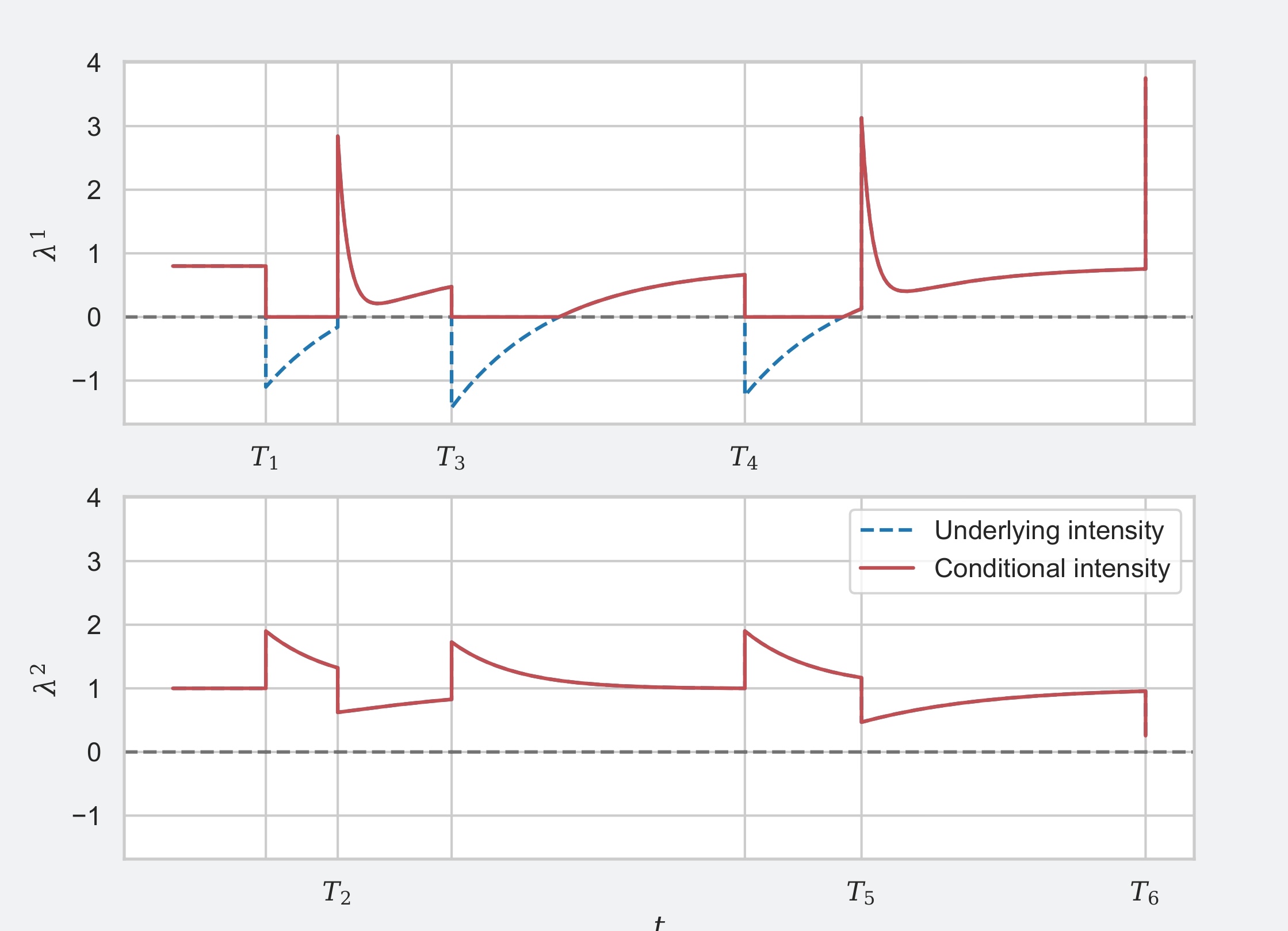
Intensity of bivariate Hawkes process with exciting and inhibiting interactions.
Activities
- (2023-2024) Representative of PhD students at graduate school (École Doctorale 386 Paris Centre).
- (2022-2023) Co-organiser of the PhD students seminar at LPSM.
Teaching
Sorbonne Université
-
(2022-2024) Statistics course, 3rd year Bachelor’s.
Topics: Parametric estimation, Maximum Likelihood Estimation, Confidence intervals, Hypothesis testing. -
(2021-2023) Data Science course, 1st year Bachelor’s.
Topics: Probability tools, Numerical optimisation, Linear regression, Supervised and non-supervised classification, Python implementations. -
(2021-2023) Advanced Mathematics course, DU RESPE (Return to higher studies Diploma for exiles).
Topics Vectors, Logic, Sequences, Complex numbers.